You are currently browsing the tag archive for the ‘Identities’ tag.
I’ve been anticipating the new detective drama Q.E.D. starring Takahashi Ai and Nakamura Aoi since it looked like it would involve a lot of awesome math, and now that the first episode is out, we can see that there is indeed a lot of awesome math! And correct, non-trivial math to boot!

Hello! Project member + stereotypical MIT nerd = WIN!

Meet Touma Sou (Nakamura), stereotypical MIT math nerd! Who, having graduated from MIT at a very early age, is for some reason reattending high school … I’m sure this will be explained in future episodes …

Mizuhara Kana (Takahashi) does an impression of MIT! D-:

Of course I am highly amused that “Massachusetts Institute of Technology” appears on the screen at the same time as Takahashi, who should definitely drop by for a visit sometime. I can show you around this place, Aichan, if you’re ever in the area.
Since “Q.E.D.” is traditionally written at the end of a math proof, this first episode of course features a math proof. As the show’s primary purpose is entertainment and not educational, it doesn’t focus on the details, but the details nevertheless are there and they’re intellectually stimulating, so I’ll cover that aspect here.

To begin with, the teacher presents the following proof in class:
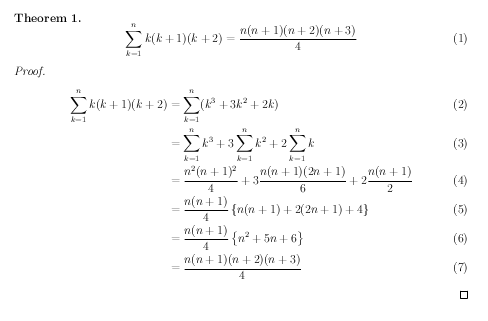
[If this is hard to read, it and the below proofs are available as a PDF.]
Let’s go through the details. The statement being proved is given in line (1). This is giving a closed-form expression for the sum of the product of three consecutive integers over a range. In line (2), the summed expression is expanded as a cubic polynomial: . This lets us use linearity of summation to split the sum into three parts (3). Then using summation identities, each of the three sums is expressed in closed form (4). In line (5), we factor out
, and in line (6), we group like terms of the remaining expression to produce a quadratic polynomial:
. This polynomial can be factored into
, leaving the desired expression (7).

Of course, for Sou this is not nearly intellectually challenging enough. (The subtitles say that the teacher’s derivation is erroneous, but it’s correct as far as I can tell; if this is what Sou actually says, maybe the producers just wanted to avoid getting into details about the distinction between generalizing a theorem and offering a better proof of the same theorem.) Sou realizes that this fact can be generalized, establishing a more powerful theorem. Instead of having a product of just three consecutive integers , why not have arbitrarily many? Sou generalizes the theorem to apply to a product of
consecutive integers:
. And indeed, there is a closed-form expression for this as well:
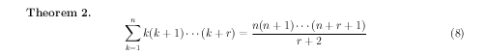
Note that this reduces to the previous theorem if you substitute .
It’s a fun exercise to try to prove this theorem, which I encourage you to do if you’re interested. I did so, and I’ll present my own proof later on. As it turns out, Sou’s proof is simpler than mine, but due to camera angles and low resolution, it’s pretty hard to actually see what the proof is.


After much squinting and deducing, I finally figured it out:
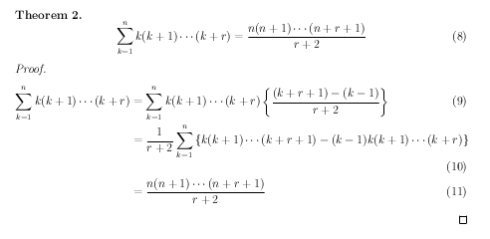
This is pretty short and makes some jumps that may not be intuitive, so I’ll go through the details:
In line (9), each term of the summation is multiplied by a ratio equal to 1, which does not change the value of the expression. You can easily do the math and see that the numerator is equal to . In line (10), the denominator of this ratio is pulled out of the summation, since it’s a constant factor, and the two terms in the numerator are multiplied with the product
, using the distributive law. Line (11) is probably the biggest jump in this proof; it’s using a telescoping sum, reducing a sum of terms by canceling out intermediate pairs. If you plug in
for
, you get
, and likewise, for
, you get
Notice that the
terms cancel when you add these together. If you keep doing this all the way to
, all the intermediate pairs cancel out, and you’re left with just two terms:
. The second term vanishes, so the overall expression is reduced to (11), which completes the proof.
The following is my own proof, which is a bit lengthier and uses binomial coefficients, along with Pascal’s second identity. Let’s first prove Pascal’s second identity, stated here as a lemma:

We use the principle of induction, which is showing that a statement holds for some base case (here ) and showing that if the statement holds for some
, then it has to hold for
as well. Putting these parts together, you prove that the statement holds for all integers greater than or equal to the base case.
Lines (13) through (17) prove the base case. This makes use of the definition of the binomial coefficient , which for
is equal to 1.
The inductive step is proved in lines (18) through (25). We assume the statement holds for and show that it also holds for
. In line (18), we split the sum of
terms into two parts. The first part is identical to the sum of
terms, which we can replace with
by the inductive assumption (19). In line (20), we replace the binomial coefficients with their equivalent factorial ratios, and in line (21), we factor
and
out of the two denominators, respectively. In lines (22) and (23), we factor out common factors of both terms, and add together the remaining fractions. Combining the two parts, we get (24), which can be written as (25), thus proving the lemma.
My alternate proof is as follows:

In line (26), we rewrite the product of consecutive integers as a ratio of factorials. We then reindex the summation (27) for convenience, so that
starts at 0. Next we multiply the entire expression by
and divide it by the same amount (28). Each term of the summation can be expressed in binomial form (29). Using Pascal’s second identity, we can rewrite the sum as (30). Turning this back into a ratio of factorials, we get (31). We can cancel out a
factor, leaving (32). Finally, expressing this ratio of factorials as a product of consecutive integers, we have (33), as desired.
(I’d stick a “Q.E.D.” at the end of that proof, but no one uses that anymore. The square box is sufficient.)
I’m definitely looking forward to more math and awesomeness in the upcoming episodes….
[The above proofs are available as a PDF.]
EDIT: Upon rewatching the episode, I discovered that Sou has excellent taste in reading material:

Douglas R. Hofstadter’s Gödel, Escher, Bach: an Eternal Golden Braid. I approve.
EDIT 2: Agggh!! What was I thinking? There’s a really easy inductive proof that I would have seen had I inducted on the right variable the first time. >_<
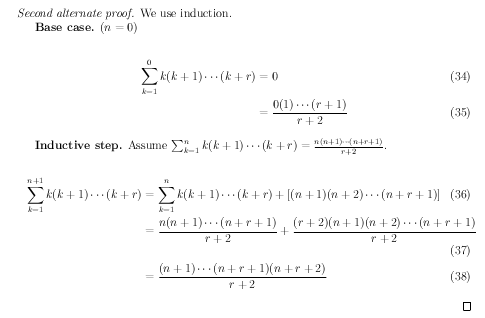
It’s, uh, self-explanatory.


Recent Comments